Code
a = sample(1:10, 10, replace = TRUE)
a [1] 8 6 5 5 6 10 9 4 1 5Tony Duan
Probability is the branch of mathematics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an event is to occur.

The sample() function is used to take a random sample from a vector. Here, we are sampling 10 numbers from the sequence 1 to 10. replace = TRUE means that after a number is drawn, it is put back into the pool and can be drawn again.
This code creates a frequency table to show how many times each number was drawn. With a small sample size, the distribution might not be perfectly even.
By increasing the sample size to 10,000, the law of large numbers suggests that the frequency of each number will be much closer to 10%.
The gtools::permutations() function calculates the number of ways to choose and arrange r items from a set of n items. The formula is n! / (n-r)!.
[,1] [,2]
[1,] 1 2
[2,] 1 3
[3,] 1 4
[4,] 2 1
[5,] 2 3
[6,] 2 4
[7,] 3 1
[8,] 3 2
[9,] 3 4
[10,] 4 1
[11,] 4 2
[12,] 4 3The number of permutations is 12.
This can be calculated manually using the formula 4! / (4-2)!.
The gtools::combinations() function calculates the number of ways to choose r items from a set of n items, where order does not matter. The formula is n! / ((n-r)! * r!).
[,1] [,2]
[1,] 1 2
[2,] 1 3
[3,] 1 4
[4,] 2 3
[5,] 2 4
[6,] 3 4The number of combinations is 6.
This can be calculated manually using the formula 4! / ((4-2)! * 2!).
Problem: The probability of any single person snoring is 20%. If there are 4 people in a room, what is the probability that at least one person snores?
This method calculates the probability of each case (1, 2, 3, or 4 people snoring) and adds them together.
There are 4 possible ways for exactly one person to snore.
There are C(4,2) = 6 ways for exactly two people to snore.
There are C(4,3) = 4 ways for exactly three people to snore.
This is a more direct method. The complement of “at least one” is “none”.
A derangement is a permutation of the elements of a set, such that no element appears in its original position.
The total number of permutations is 4! = 24.
The number of derangements D(n) can be approximated by round(n!/e). For n=4, this is D(4) = 9.
The probability of a complete derangement is the number of derangements divided by the total number of permutations.
First, choose 1 number to be correct (C(4,1) = 4 ways). Then, find the number of derangements for the remaining 3 numbers (D(3) = 2).
The total number of ways to get exactly 1 correct is C(4,1) * D(3) = 4 * 2 = 8.
First, choose 2 numbers to be correct (C(4,2) = 6 ways). Then, find the number of derangements for the remaining 2 numbers (D(2) = 1).
This is impossible. If 3 numbers are in their correct positions, the 4th number must also be in its correct position. The number of derangements of 1 item is D(1) = 0.
There is only one way for this to happen.
The sum of all probabilities should be 1.
The binomial distribution models the number of successes in a fixed number of independent trials, each with a binary outcome (success/failure).
In R, the dbinom function calculates the probability of getting exactly x successes. While this is technically a PMF for a discrete distribution, R uses the d prefix convention for both PDF (continuous) and PMF (discrete).
Probability of exactly 1 person snoring:
[1] 0.4096Probabilities for 0, 1, 2, 3, or 4 people snoring:
The pbinom function calculates the cumulative probability of getting q or fewer successes.
Probability of 1 or fewer people snoring:
The rbinom function generates random numbers from a binomial distribution.
Generate 10,000 random values from this distribution:
A continuous probability distribution characterized by a bell-shaped curve. It is defined by its mean (μ) and standard deviation (σ).
dnorm: Density function (PDF)pnorm: Cumulative distribution function (CDF)qnorm: Quantile function (inverse CDF)rnorm: Random number generationCalculates the height of the probability density function at a given point.
Calculates the area under the curve to the left of a given value (the probability of observing a value less than or equal to q).
Probability of observing a value <= 70 from a N(75, 5) distribution:
Finds the value x such that P(X <= x) = p. It is the inverse of the CDF.
Find the 25th percentile (Q1) of a N(75, 5) distribution:
Generate 1,000 random numbers from a N(75, 5) distribution and plot a histogram.
It’s often important to check if a dataset follows a normal distribution.
A bell-shaped histogram suggests normality.
If the data is normal, the points on a Q-Q plot will fall closely along the straight line.
A statistical test for normality. The null hypothesis (H0) is that the data is normally distributed.
If the p-value is > 0.05, we do not reject the null hypothesis.
If the p-value is < 0.05, we reject the null hypothesis.
https://www.huber.embl.de/users/kaspar/biostat_2021/2-demo.html
https://www.youtube.com/watch?v=peEsXbdMY_4
https://www.youtube.com/watch?v=ETd-jPhI_tE
https://www.youtube.com/watch?v=kvmSAXhX9Hs
https://www.youtube.com/watch?v=RlhnNbPZC0A
https://www.youtube.com/watch?v=X5NXDK6AVtU
https://www.scribbr.com/statistics/probability-distributions/#:~:text=A%20probability%20distribution%20is%20a,using%20graphs%20or%20probability%20tables.
https://www.youtube.com/watch?v=Q_pO9NzWxPY
https://www.statology.org/test-for-normality-in-r/
https://en.wikipedia.org/wiki/Derangement
R version 4.5.1 (2025-06-13)
Platform: aarch64-apple-darwin20
Running under: macOS Sequoia 15.5
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
time zone: Asia/Shanghai
tzcode source: internal
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] gtools_3.9.5
loaded via a namespace (and not attached):
[1] htmlwidgets_1.6.4 compiler_4.5.1 fastmap_1.2.0 cli_3.6.5
[5] tools_4.5.1 htmltools_0.5.8.1 rstudioapi_0.17.1 yaml_2.3.10
[9] rmarkdown_2.29 knitr_1.50 jsonlite_2.0.0 xfun_0.52
[13] digest_0.6.37 rlang_1.1.6 evaluate_1.0.3 ---
title: "Probability"
author: "Tony Duan"
execute:
warning: false
error: false
format:
html:
toc: true
toc-location: right
code-fold: show
code-tools: true
number-sections: true
code-block-bg: true
code-block-border-left: "#31BAE9"
---
Probability is the branch of mathematics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an event is to occur.
{width="350"}
# Random Numbers
## Draw 10 numbers from 1 to 10
The `sample()` function is used to take a random sample from a vector. Here, we are sampling 10 numbers from the sequence 1 to 10. `replace = TRUE` means that after a number is drawn, it is put back into the pool and can be drawn again.
```{r}
a = sample(1:10, 10, replace = TRUE)
a
```
This code creates a frequency table to show how many times each number was drawn. With a small sample size, the distribution might not be perfectly even.
```{r}
as.data.frame(table(a))
```
## Draw 10,000 numbers from 1 to 10
By increasing the sample size to 10,000, the law of large numbers suggests that the frequency of each number will be much closer to 10%.
```{r}
a = sample(1:10, 10000, replace = TRUE)
```
```{r}
as.data.frame(table(a))
```
# Permutations and Combinations

## Permutations (order matters): choosing 2 numbers from 4
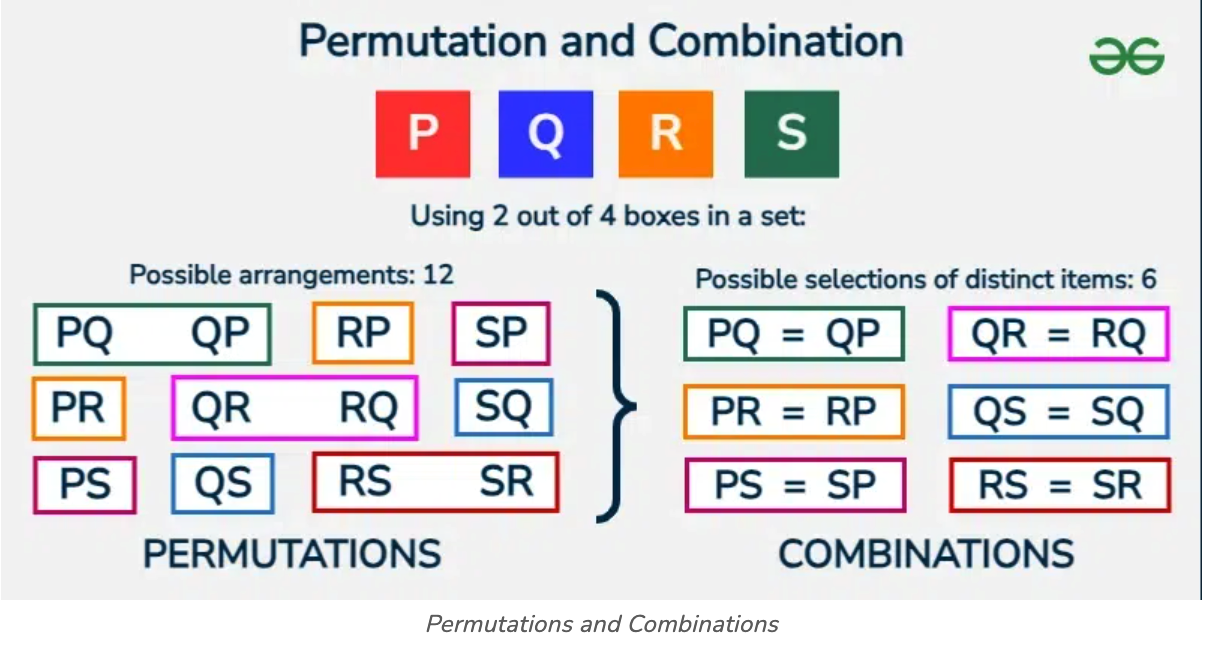
The `gtools::permutations()` function calculates the number of ways to choose and arrange `r` items from a set of `n` items. The formula is n! / (n-r)!.
```{r}
library(gtools)
all_num = 4
choose = 2
res <- permutations(n = all_num, r = choose, v = 1:all_num)
res
```
The number of permutations is 12.
```{r}
print(nrow(res))
```
This can be calculated manually using the formula 4! / (4-2)!.
```{r}
factorial(4) / factorial(4 - 2)
```
## Combinations (order does not matter): choosing 2 numbers from 4
The `gtools::combinations()` function calculates the number of ways to choose `r` items from a set of `n` items, where order does not matter. The formula is n! / ((n-r)! * r!).
```{r}
library(gtools)
all_num = 4
choose = 2
res <- combinations(n = all_num, r = choose, v = 1:all_num)
res
```
The number of combinations is 6.
```{r}
print(nrow(res))
```
This can be calculated manually using the formula 4! / ((4-2)! * 2!).
```{r}
factorial(4) / (factorial(4 - 2) * factorial(2))
```
# Conditional Probability
**Problem**: The probability of any single person snoring is 20%. If there are 4 people in a room, what is the probability that at least one person snores?
```{r}
p = 0.2
n = 4
```
## Solution 1: P(at least one) = P(1 snoring) + P(2 snoring) + P(3 snoring) + P(4 snoring)
This method calculates the probability of each case (1, 2, 3, or 4 people snoring) and adds them together.
### 0 snoring
```{r}
p0 = (0.8 * 0.8 * 0.8 * 0.8)
p0
```
### 1 snoring
There are 4 possible ways for exactly one person to snore.
```{r}
p1 = (0.2 * 0.8 * 0.8 * 0.8) * 4
p1
```
### 2 snoring
There are C(4,2) = 6 ways for exactly two people to snore.
```{r}
factorial(4) / (factorial(4 - 2) * factorial(2))
```
```{r}
p2 = (0.2 * 0.2 * 0.8 * 0.8) * 6
p2
```
### 3 snoring
There are C(4,3) = 4 ways for exactly three people to snore.
```{r}
factorial(4) / (factorial(4 - 3) * factorial(3))
```
```{r}
p3 = (0.2 * 0.2 * 0.2 * 0.8) * 4
p3
```
### 4 snoring
```{r}
p4 = (0.2 * 0.2 * 0.2 * 0.2)
p4
```
### Total probability of at least one person snoring:
```{r}
P_at_least_one = p1 + p2 + p3 + p4
P_at_least_one
```
## Solution 2: P(at least one) = 1 - P(no one snoring)
This is a more direct method. The complement of "at least one" is "none".
```{r}
P_at_least_one2 = 1 - (0.8^4)
P_at_least_one2
```
# Derangement Problem
A derangement is a permutation of the elements of a set, such that no element appears in its original position.
## Question 1: What is the probability of choosing 4 numbers from 4 and getting 0 correct (all wrong)?
The total number of permutations is 4! = 24.
```{r}
factorial(4)
```
The number of derangements D(n) can be approximated by `round(n!/e)`. For n=4, this is D(4) = 9.
```{r}
e = exp(1) # Use the built-in constant for e
D_4 = round(factorial(4) / e)
D_4
```
The probability of a complete derangement is the number of derangements divided by the total number of permutations.
```{r}
Q1 = D_4 / factorial(4)
Q1
```
## Question 2: What is the probability of choosing 4 numbers from 4 and getting exactly 1 correct?
First, choose 1 number to be correct (C(4,1) = 4 ways). Then, find the number of derangements for the remaining 3 numbers (D(3) = 2).
```{r}
D_3 = round(factorial(3) / e)
D_3
```
The total number of ways to get exactly 1 correct is C(4,1) * D(3) = 4 * 2 = 8.
```{r}
Q2 = (4 * D_3) / factorial(4)
Q2
```
## Question 3: What is the probability of choosing 4 numbers from 4 and getting exactly 2 correct?
First, choose 2 numbers to be correct (C(4,2) = 6 ways). Then, find the number of derangements for the remaining 2 numbers (D(2) = 1).
```{r}
D_2 = round(factorial(2) / e)
C_4_2 = factorial(4) / (factorial(2) * factorial(2))
Q3 = (C_4_2 * D_2) / factorial(4)
Q3
```
## Question 4: What is the probability of choosing 4 numbers from 4 and getting exactly 3 correct?
This is impossible. If 3 numbers are in their correct positions, the 4th number must also be in its correct position. The number of derangements of 1 item is D(1) = 0.
```{r}
Q4 = 0
Q4
```
## Question 5: What is the probability of choosing 4 numbers from 4 and getting all 4 correct?
There is only one way for this to happen.
```{r}
Q5 = 1 / factorial(4)
Q5
```
The sum of all probabilities should be 1.
```{r}
Q1 + Q2 + Q3 + Q4 + Q5
```
# Distributions
## Binomial Distribution
The binomial distribution models the number of successes in a fixed number of independent trials, each with a binary outcome (success/failure).
### Probability Mass Function (PMF)
In R, the `dbinom` function calculates the probability of getting exactly `x` successes. While this is technically a PMF for a discrete distribution, R uses the `d` prefix convention for both PDF (continuous) and PMF (discrete).
Probability of exactly 1 person snoring:
```{r}
n = 4 # number of trials (people)
p = 0.2 # probability of success (snoring)
dbinom(x = 1, size = n, prob = p)
```
Probabilities for 0, 1, 2, 3, or 4 people snoring:
```{r}
dbinom(x = c(0, 1, 2, 3, 4), size = n, prob = p)
```
### Cumulative Distribution Function (CDF)
The `pbinom` function calculates the cumulative probability of getting `q` or fewer successes.
Probability of 1 or fewer people snoring:
```{r}
pbinom(q = 1, size = n, prob = p, lower.tail = TRUE)
```
### Random Number Generation
The `rbinom` function generates random numbers from a binomial distribution.
Generate 10,000 random values from this distribution:
```{r}
a = rbinom(10000, size = 4, prob = 0.2)
table(a)
```
## Normal Distribution (Gaussian Distribution)
A continuous probability distribution characterized by a bell-shaped curve. It is defined by its mean (μ) and standard deviation (σ).
### R Functions
- `dnorm`: Density function (PDF)
- `pnorm`: Cumulative distribution function (CDF)
- `qnorm`: Quantile function (inverse CDF)
- `rnorm`: Random number generation
### Probability Density Function (PDF)
Calculates the height of the probability density function at a given point.
```{r}
dnorm(0, mean = 1, sd = 2)
```
### Cumulative Distribution Function (CDF)
Calculates the area under the curve to the left of a given value (the probability of observing a value less than or equal to `q`).
Probability of observing a value <= 70 from a N(75, 5) distribution:
```{r}
pnorm(q = 70, mean = 75, sd = 5)
```
### Quantile Function
Finds the value `x` such that P(X <= x) = p. It is the inverse of the CDF.
Find the 25th percentile (Q1) of a N(75, 5) distribution:
```{r}
qnorm(p = 0.25, mean = 75, sd = 5)
```
### Random Number Generation
Generate 1,000 random numbers from a N(75, 5) distribution and plot a histogram.
```{r}
nd = rnorm(n = 1000, mean = 75, sd = 5)
hist(nd)
```
### Checking for Normality
It's often important to check if a dataset follows a normal distribution.
```{r}
nd_data = rnorm(n = 1000, mean = 0, sd = 2)
non_nd_data = rpois(n = 1000, lambda = 5) # Poisson data is not normal
```
#### Method 1: Histogram
A bell-shaped histogram suggests normality.
```{r}
par(mfrow = c(1, 2))
hist(nd_data, col = 'steelblue', main = 'Normal')
hist(non_nd_data, col = 'darkred', main = 'Non-normal')
```
#### Method 2: Q-Q Plot
If the data is normal, the points on a Q-Q plot will fall closely along the straight line.
```{r}
par(mfrow = c(1, 2))
qqnorm(nd_data, main = 'Normal')
qqline(nd_data)
qqnorm(non_nd_data, main = 'Non-normal')
qqline(non_nd_data)
```
#### Method 3: Shapiro-Wilk Test
A statistical test for normality. The null hypothesis (H0) is that the data is normally distributed.
If the p-value is > 0.05, we do not reject the null hypothesis.
```{r}
shapiro.test(nd_data)
```
If the p-value is < 0.05, we reject the null hypothesis.
```{r}
shapiro.test(non_nd_data)
```
## Other Key Distributions
- **Student's t-distribution**: Used for inference about the mean of a normally distributed population when the standard deviation is unknown.
- **F-distribution**: Used in ANOVA to compare the means of multiple groups.
- **Chi-square distribution**: Used in goodness-of-fit tests and tests of independence.
- **Poisson Distribution**: Models the number of events occurring in a fixed interval of time or space.
# References
https://www.huber.embl.de/users/kaspar/biostat_2021/2-demo.html
https://www.youtube.com/watch?v=peEsXbdMY_4
https://www.youtube.com/watch?v=ETd-jPhI_tE
https://www.youtube.com/watch?v=kvmSAXhX9Hs
https://www.youtube.com/watch?v=RlhnNbPZC0A
https://www.youtube.com/watch?v=X5NXDK6AVtU
https://www.scribbr.com/statistics/probability-distributions/#:~:text=A%20probability%20distribution%20is%20a,using%20graphs%20or%20probability%20tables.
https://www.youtube.com/watch?v=Q_pO9NzWxPY
https://www.statology.org/test-for-normality-in-r/
https://en.wikipedia.org/wiki/Derangement
```{r, attr.output='.details summary="sessionInfo()"'}
sessionInfo()
```